Un algoritmo concido para detectar ciclos infinitos en listas enlazadas es el algoritmo de Floyd (la tortuga y la liebre)
En este artículo haremos una explicación resumida de este algoritmo.
Contenido
Definición del Problema
Una lista enlazada es una estructura de datos compuesta por elementos dispuestos de forma secuencial donde un nodo apunta a un siguiente nodo y así sucesivamente hasta llegar a un nodo vacío.
Una representación sencilla sería esta:

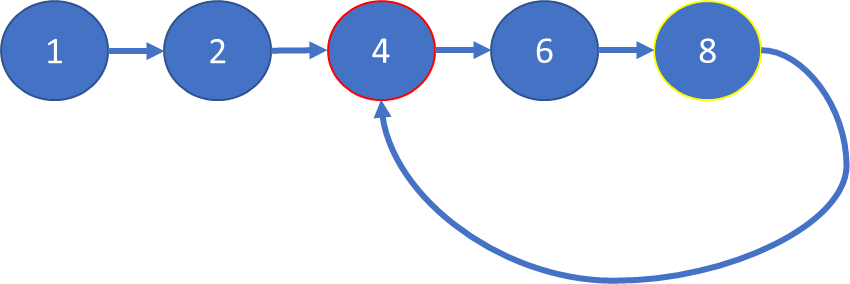
En la ilustración anterior el nodo (1) apunta al nodo (2) el que a su vez apunta al nodo (4) que apunta al nodo (6) el cual apunta al nodo (8) que finalmente apunta a NULL como elemnto vacío.
Una variante de esta estructura sería una lista enlazada con un ciclo en la cual no hay un nodo final NULL sino que uno de los nodos es referenciado por dos nodos.
En JavaScript, cada nodo puede ser implementado mediante un objeto que tenga dos propiedades: data y next, donde next es un puntero hacia otro nodo o hacia null.
{ data: 1, next: null }
Dado que en el manejo de listas enlazadas se suele utilizar la presencia del valor next:null para detectar el último nodo de la lista, en el caso de listas enlazadas con ciclo se dificulta la posibilidad de detectar dónde termina la lista, dado que esta no termina realmente.
Una forma de resolver este problema es la detección del ciclo y la identificación del nodo ciclado mediante lo que se conoce como el método «ingénuo» que consiste en llevar un registro de cada nodo visitado y detectar el fin de la lista cuando se visita un nodo por segunda vez. Se conoce como ingénuo dado que es bastante ineficiente y poco escalable.
Una segunda forma es el algoritmo ideado por Robert W Floyd, el cual consiste en escanear la estructura de datos mediante dos punteros, uno más rápido que otro, y detectar el ciclo cuando ambos punteros refieran al mismo nodo. Este ingenioso algoritmo es altamente eficiente y escalable.
El algoritmo de la tortuga y la liebre
El algoritmo de la tortuga y la liebre, como también se conoce al algoritmo de Floyd, tiene como objetivo identificar si una lista enlazada se encuentra ciclada; se puede dividir en dos partes: una primera parte para detectar el ciclo y una segunda parte para encontrar el nodo donde se origina el ciclo.
Primera Parte: Detectar el ciclo
La primera parte de este algoritmo consiste en atravezar la lista enlazada con dos punteros, la tortuga (T) que atravieza la lista «despacio» un nodo a la vez y la liebre (L) que atraviesa la lista «rápido» dos nodos en cada iteración; en algún momento la liebre termina alcanzando a la tortuga y coincidiendo en el mismo nodo lo cual nos indica que estamos ante una lista enlazada y ciclada.

En la ilustración anterior, en la primera línea («--«) se muestra la lista enlazada y cómo se repite una y otra vez de forma secuencial por causa de el ciclo definido en el nodo 8 hacia el nodo 4.
Seguidamente en esa misma ilustración se muestran las iteraciones individuales donde los punteros T y L, comienzan en el mismo punto (nodo 1) en la iteración #1 y se mueven a distintas velocidades (T de uno en uno, y L de 2 en 2). De esta forma T y L terminan apuntando al mismo nodo (nodo6) en la iteración #4.
Segunda Parte: Encontrar el nodo inicial
En la segunda parte del algoritmo, se utilizan otros dos punteros p1 y p2, donde p1 inicia desde el primer nodo de la lista y p2 inicia desde el nodo donde coincidieron T y L. Se hace avanzar cada puntero un nodo a la vez hasta que ambos coinciden en un mismo nodo. Este nodo es el primer nodo del ciclo.
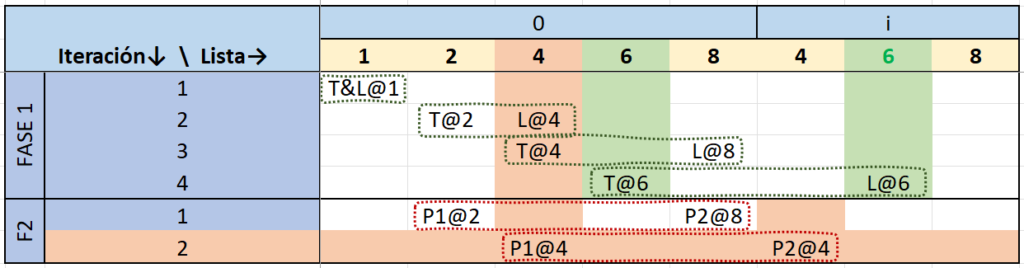
La figura 4 ilustra ambas fases para nuestro ejemplo. En la fase 1 en las iteraciones de la 1 a la 4 se resuelve detectar que se trata de un ciclo; las áreas color verde demarcan el resultado de esta primera fase donde ambos punteros T y L apuntan al nodo 6. Al coincidir, quiere decir que estamos ante la presencia de un ciclo.
En la fase 2 se inicializan dos punteros P1 y P2 y avanzan un nodo a la vez hasta coincidir en la iteración #2 de esta fase, en el nodo 4 que en efecto corresponde al primer nodo dentro del ciclo creado por el nodo 8. El resultado de esta segunda fase se demarca mediante las áreas de color naranja.
Dado que con este mecanismo no es necesario llevar ninguna estructura de datos escalable paralela sino solamente un par de punteros, se considera que es altamente eficiente al tener una complejidad de O(N) en tiempo y O(1) en espacio.
Implementación en JavaScript
El siguiente listado muestra una implementación funcional en JavaScript. Puedes encontrar una versión actualizada en mi paquete de npm jn-didactic la cual incluye pruebas unitarias que muestran una diferencia entre los algoritmos ingénuo (naive) y Floyd al correrlos para una lista de 10 millones de elementos.
También puedes clonar el código fuente directamente desde GitHub:
https://github.com/janunezc/jn-didactic
function detectCycle_Floyd(head, cycleLimit) {
let pT = head;
let pL = head;
let cycleCount = 0;
while (true) { // FASE 1 DETECTAR EL CICLO
if ((cycleLimit && cycleCount > cycleLimit) || (pL === null || pL.next === null || pL.next.next === null)) return false;
pT = pT.next; //1+
pL = pL.next.next; //2+
if (pT.data === pL.data) break; //CYCLE FOUND
cycleCount++;
}
let p1 = head;
let p2 = pT;
let previousNode = p2;
cycleCount = 0;
while (true) { // FASE 2 - ENCONTRAR EL NODO
if (p1.data === p2.data) return previousNode;
previousNode = p2;
p1 = p1.next;
p2 = p2.next;
if (cycleLimit && cycleCount > cycleLimit) return false;
cycleCount++;
}
}
![]()
Comentarios