Notación Asintótica (Big O) Explicación y Ejemplos

En ciencias de la computación se conoce como notación asintótica o notación «O grande» a la forma de describir el crecimiento de los requerimientos de recursos (ciclos de procesamiento, tiempo, memoria, almacenamiento) de un algoritmo respecto del tamaño de los datos de entrada, o más explicitamente respecto del tamaño del trabajo a procesar.

En esta publicación realizamos algunas explicaciones sobre el tema y mostramos ejemplos en código sobre dicha notación

Conceptos Fundamentales

Primero vamos a repasar algunos conceptos relacionados con este tema:

1. Algoritmo: Se refiere a un procedimiento que recibe unos datos de entrada, realiza un trabajo sobre esos datos y devuelve un resultado. Usualmente se usa el término algoritmo en ciencias de la computación de forma intercambiable con los conceptos de función o método.
   
2. Datos de entrada: Son los datos que se brindan a un algoritmo dado para realizar el proceso o trabajo correspondiente. Un detalle importante a considerar es que, aun cuando usualmente el tamaño de la entrada se pueda medir en bytes o cantidad de datos, la realidad es que en ocasiones no se trata de la cantidad de datos sino de la laboriosidad que los datos de entrada representan para el algoritmo; por ejemplo, puede que nuestro algoritmo reciba un dato de entrada que es de un solo tamaño (digamos un entero) pero ese entero cuando es un número grande (digamos 1 millón) hace que el trabajo a realizar tome más tiempo que si se trata de un número pequeño (digamos 10 unidades)
   
3. Tiempo de ejecución, ciclos de ejecución: Para nuestro análisis se refiere al tiempo que toma a un algoritmo realizar la tarea para la cual está diseñado. Este tiempo depende no solo del tamaño de la entrada y del diseño del algoritmo, sino también de variables tales como la velocidad del hardware entre otras. Es por esto que una medida más precisa sería ciclos de ejecución o complejidad de ejecución que define el tamaño relativo de la tarea a realizar respecto de la especificación en los datos de entrada.
   
4. Requerimiento de espacio: En este caso se refiere a la cantidad de memoria RAM y/o memoria de almacenamiento persitente que se necesita por parte de un algoritmo dado para realizar su trabajo. Al igual que con el tiempo de ejecución, el espacio requerido no solamente depende del tamaño de la entrada o el diseño del algoritmo, sino de otras variables relacionadas con el hardware.

Explicación de la notación asintótica

La palabra asíntota se define como literalmente como «Dicho de una curva : Que se acerca indefinidamente a una recta o a otra curva sin llegar nunca a encontrarla» (rae, wikipedia).

La notación asintótica es una forma de describir una curva matemática, una forma de evolución de un fenómeno respecto a cambios en sus factores de entrada. También se le conoce como notación de «O grande» o notación de «Cota Superior» (wikipedia)

Dado que en la ejecución de un algoritmo para realizar una tarea con base en una entrada determinada, el tiempo y espacio requeridos para la ejecución de la tarea dependen de muchas variables, en lugar de definir un tiempo o espacio específicos se utiliza una notación que describa cómo crecerán esos requerimientos de espacio y tiempo, respecto de la entrada recibida.

Tal como describe wikipedia, se han definido algunas expresiones u «órdenes» usuales para describir las formas de crecimiento más comunes:

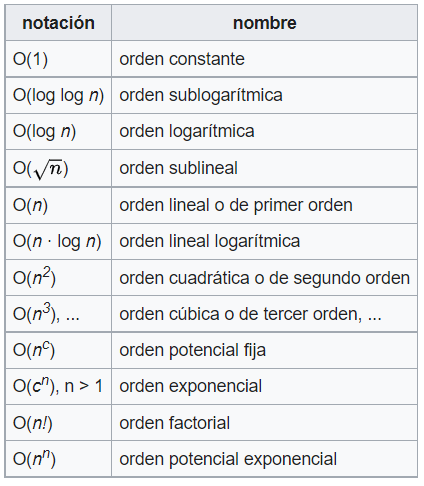
Algunos Órdenes Comunes

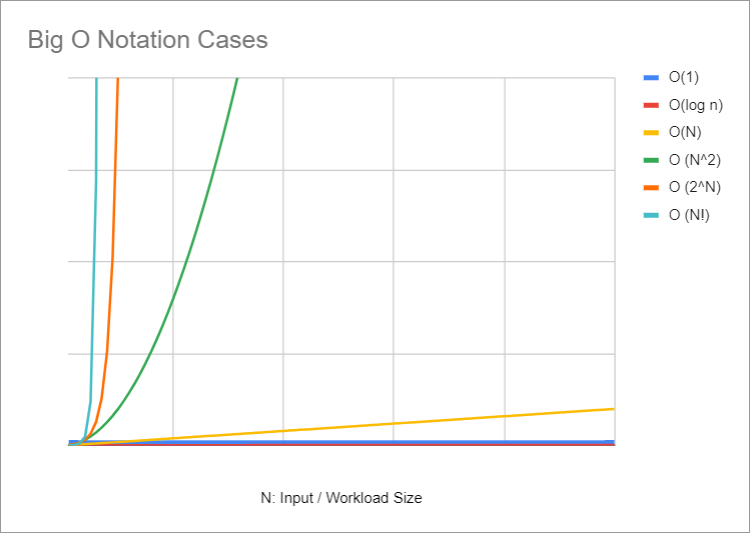
Como se observa en la figura 1 (inspirada en https://www.bigocheatsheet.com/) algunas órdenes asintóticas como O(1) u O(log n) mantienen una demanda de requerimientos (operaciones o espacio) bastante pequeños conforme aumenta el tamaño de la entrada; mientras que otras como O(N^2) u O(2^N) u O(N!) aumentan de forma significativa, casi que prohibitiva, conforme aumenta el tamaño de las entradas.

Algunos ejemplos de código comunes

En las siguientes sub-secciones mostramos ejemplos de código que usualmente se representan con notaciones asintóticas comunes.

Orden Constante ● O(1)

Así, O(1) describe un algoritmo que siempre toma el mismo esfuerzo (en tiempo o espacio) independientemente de la entrada. Un ejemplo de esto sería una función que devueleve el primer elemento de un arreglo.

Imaginemos dos arreglos: uno llamado «arregloGrande» contiene 2 millones de elementos mientras que uno llamado «arregloChico» tiene solamente 3 elementos.

Ahora imaginemos una función llamada «funcionConstante» la cual no toma para nada en cuenta el arreglo de entrada y siempre devuelve el mismo valor literal 123.

let arregloMuyGrande = [];
for(i=0;i<10000000;i++){arregloMuyGrande.push(`A`);} //Agrega 1MM de entradas

function obtenerPrimerElemento(entrada){
   return entrada[0];
}

for(i=500000; i<=10000000;i+=500000){
   let arreglo = arregloMuyGrande.slice(1,i);
   console.time(`BUCKET ${i}`);
   obtenerPrimerElemento(arreglo);
   console.timeEnd(`BUCKET ${i}`);
}

Bajo este ejemplo, en un mundo ideal, la función siempre tomará el mismo tiempo en ejecutarse independientemente del tamaño de la entrada.

Veamos el resultado:

BUCKET  500000: 0.078ms
BUCKET 1000000: 0.006ms
BUCKET 1500000: 0.009ms
BUCKET 2000000: 0.005ms
BUCKET 2500000: 0.013ms
BUCKET 3000000: 0.015ms
BUCKET 3500000: 0.008ms
BUCKET 4000000: 0.011ms
BUCKET 4500000: 0.012ms
BUCKET 5000000: 0.011ms
BUCKET 5500000: 0.01 ms
BUCKET 6000000: 0.008ms
BUCKET 6500000: 0.015ms
BUCKET 7000000: 0.013ms
BUCKET 7500000: 0.015ms
BUCKET 8000000: 0.01 ms
BUCKET 8500000: 0.014ms
BUCKET 9000000: 0.012ms
BUCKET 9500000: 0.021ms
BUCKET 1000000: 0.01 ms

En este resultado vemos que una gran cantidad de las muestras toman aproximadamente 12ns en devolver el primer elemento, salvo varias excepciones.

Veámoslo ahora en modo gráfico:

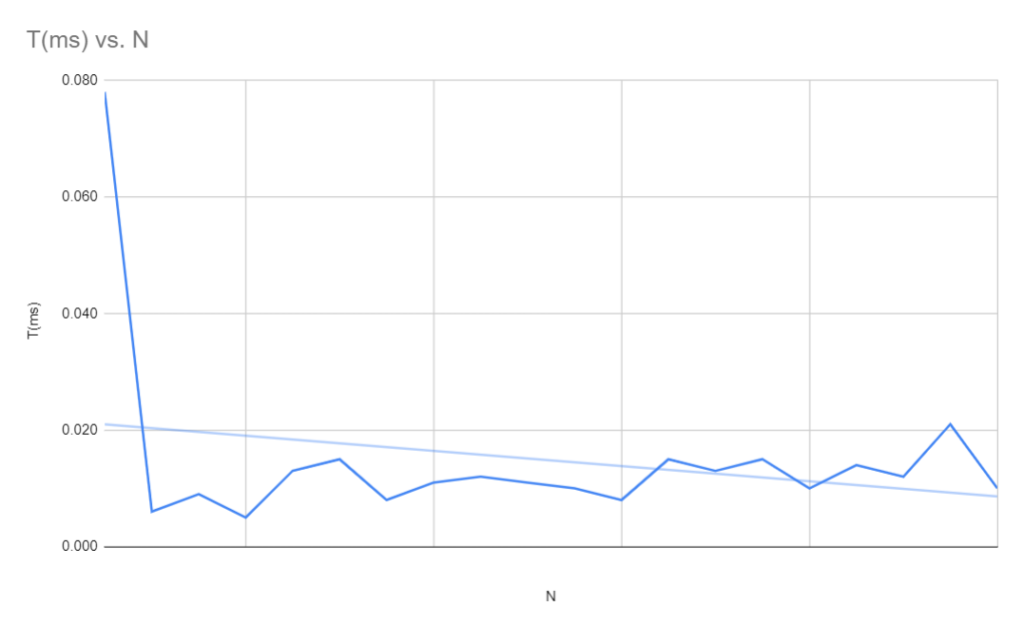
En la figura anterior vemos el gráfico de nuestra ejecución que se mantiene prácticamente constante entre 8ns y 12ns, con la excepción de la primera muestra (80ns) que evidentemente carga con la inicialización de todo el proceso de manejo de los datos en memoria.

Orden Lineal o de Primer Orden ● O(n)

El siguiente orden a considerar es el llamado primer orden o lineal para el cual la complejidad del trabajo crecerá proporcionalmente al crecimiento de la especificación de entrada.

Si consideramos un algoritmo que ejecuta siempre la misma cantidad de operaciones para cada elemento de trabajo de la entrada, estaremos ante un algoritmo con una complejidad de O(n).

El siguiente código de ejemplo muestra una aproximación teórica a este orden lineal.

Tenemos una función agregarPunto() que opera sobre un arreglo de cadenas. Todas las cadenas son siempre iguales "A" para facilitar el ejemplo. La función solamente agrega un punto "." a cada elemento del arreglo recibido.

Se definen 3 arreglos a saber: arregloChico con solo 10 elementos, arregloGrande con un millón de elementos y arregloMuyGrande con diez millones de elementos.

let arregloChico  = [];
for(i=0;i<10;i++){arregloChico.push(`A`);} //Agrega 10 entradas

let arregloGrande = [];
for(i=0;i<1000000;i++){arregloGrande.push(`A`);} //Agrega 1MM de entradas

let arregloMuyGrande = [];
for(i=0;i<10000000;i++){arregloMuyGrande.push(`A`);} //Agrega 1MM de entradas

function agregarPunto(entrada) {
   return entrada.map(item => item + ".");
}

console.time("CHICO");
agregarPunto(arregloChico);
console.timeEnd("CHICO", arregloChico.length);
console.log("  TAMANO:", arregloChico.length);

console.time("GRANDE");
agregarPunto(arregloGrande);
console.timeEnd("GRANDE", arregloGrande.length);
console.log("  TAMANO:", arregloGrande.length);

console.time("MUY_GRANDE");
agregarPunto(arregloMuyGrande);
console.timeEnd("MUY_GRANDE");
console.log("  TAMANO:", arregloMuyGrande.length);

Decimos que es una aproximación teórica porque aun cuando la función realiza la misma operación para cada elemento de la entrada, siendo una complejidad de O(n) varios factores dentro del ambiente de ejecución hacen que no sea exactamente una relación lineal.

En nuestro ambiente de pruebas estos fueron los resultados:

CHICO: 0.097ms
   TAMANO: 10
GRANDE: 142.658ms
   TAMANO: 1000000
MUY_GRANDE: 1.004s
   TAMANO: 10000000

Así, para 10 entradas el procedimiento tardó poco menos de 0.100ms, lo que representa 0.010ms (10ns) por cada elemento del arreglo de entrada.

Para 1 millón de entradas el proceso tardó 143.658ms lo que representa 0.000143ms (0.1ns) por cada elemento de la entrada.

Para 10 millones de entradas el proceso tardó poco más de 1000ms, es decir 0.001 (1ns) por cada elemento.

Así aun cuando en teoría esperábamos que el crecimiento fuera lineal, el caso es que no lo es ya que el tiempo de ejecución por cada elemento de la entrada varía dependiendo del caso entre 10ns para el arreglo chico, 0.1ns (muy rápido) para el arreglo grande y 1ns para el arreglo muy grande.

Un análisis de O(N) más detallado

Bajo esta misma linea teórica, si consideramos el siguiente código, realiza la misma operación, pero analizamos sub conjuntos cada uno con 500mil elementos más que el anterior:

let arregloMuyGrande = [];
for(i=0;i<10000000;i++){arregloMuyGrande.push(`A`);} //Agrega 1MM de entradas

function agregarPunto(entrada) {
   return entrada.map(item => item + ".");
}

for(i=0; i<=10000000;i+=500000){
   let arreglo = arregloMuyGrande.slice(1,i);
   console.time(`BUCKET ${i}`);
   agregarPunto(arreglo);
   console.timeEnd(`BUCKET ${i}`);
}

En este caso el resultado es bastante revelador:

BUCKET 0: 0.087ms
BUCKET 500000: 10.753ms
BUCKET 1000000: 80.544ms
BUCKET 1500000: 151.339ms
BUCKET 2000000: 214.029ms
BUCKET 2500000: 226.784ms
BUCKET 3000000: 327.949ms
BUCKET 3500000: 349.375ms
BUCKET 4000000: 415.787ms
BUCKET 4500000: 439.536ms
BUCKET 5000000: 772.352ms
BUCKET 5500000: 629.745ms
BUCKET 6000000: 576.067ms
BUCKET 6500000: 744.979ms
BUCKET 7000000: 1.045s
BUCKET 7500000: 745.408ms
BUCKET 8000000: 795.295ms
BUCKET 8500000: 944.341ms
BUCKET 9000000: 1.130s
BUCKET 9500000: 917.629ms
BUCKET 10000000: 1.353s

Tenemos entonces 21 muestras de ejecución. Vemos cómo la muestra de 3.5 millones de elementos tardó 349ms, mientras que la de 4.5 millones de elementos tardó 439ms, y la de 8 millones de elementos tardó 795ms. Si lo graficamos luce así:

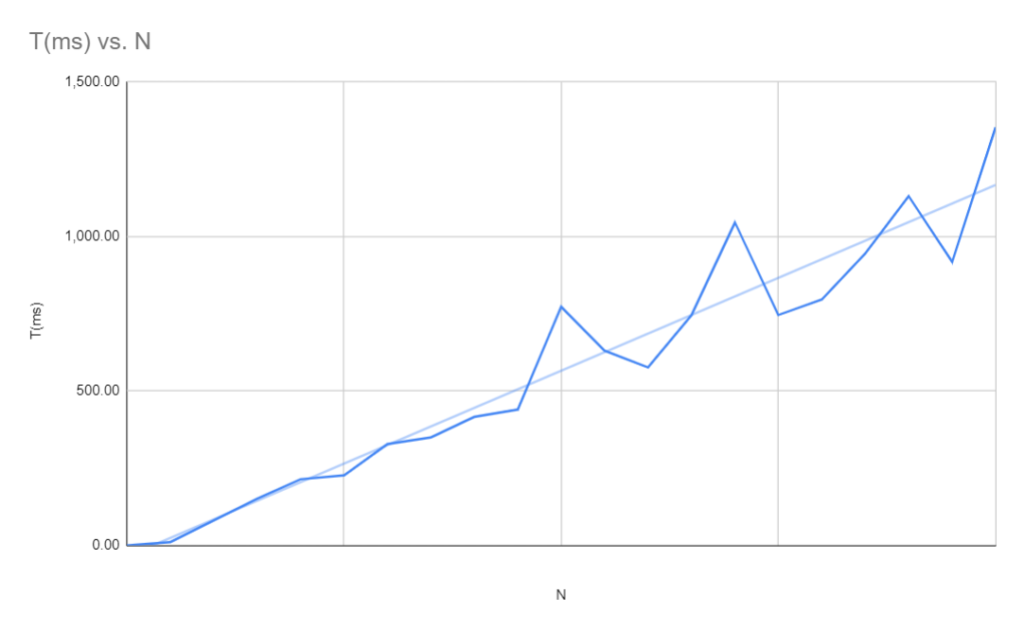
En esta figura 2 vemos que en realidad el crecimiento tiene una tendencia lineal, aunque cada muestra se ve afectada por otras variables que no son determinísticas para nuestro análisis.

Orden Logarítmico ● O(log n)

Consideremos ahora el orden logarítmico. Su principal característica es que el crecimiento de los recursos requeridos tiende a disminuir y a volverse constante conforme se aumenta el tamaño de la entrada.

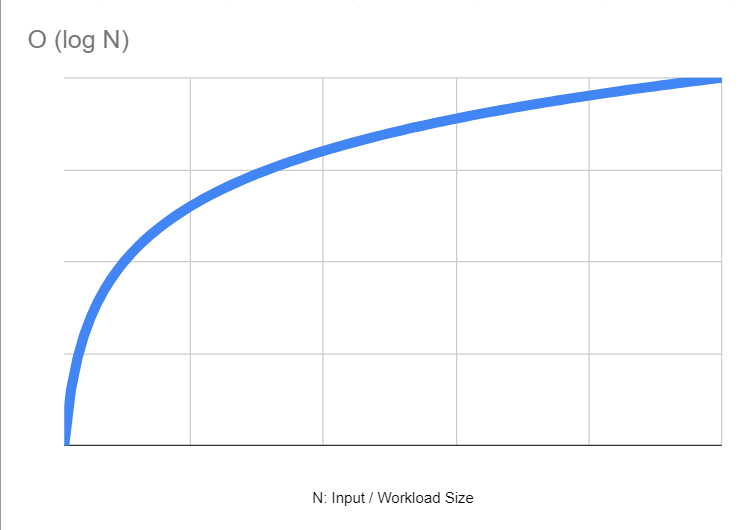
Se dice que las búsquedas binarias sobre elementos ordenados tienden a tener una complejidad logarítmica ya que tienden a tener un mejor desempeño conforme crecen los datos de entrada.

 11,707 total views,  1 views today